I have just finished setting up handling for AR(1) and compound symmetry variance structures in my maximum likelihood estimation function for matrix variate normal distributions in matrixdist. This means I may submit it to CRAN soon (it’s currently available on github). An example:
library(MixMatrix)
A <- rmatrixnorm(100, mean=array(0,dim=c(3,4)), U = toeplitz(c(1,.8,.64)), V = rWishart(1,7,diag(4))[,,1])
MLmatrixnorm(A, row.variance="AR(1)")$mean
[,1] [,2] [,3] [,4]
[1,] 0.2993834 0.05670813 0.4119235 0.2035769
[2,] 0.3010836 0.06080098 0.2285708 0.1158808
[3,] 0.1447031 0.17038166 0.2758068 0.2638911
$U
[,1] [,2] [,3]
[1,] 1.0000000 0.770081 0.5930248
[2,] 0.7700810 1.000000 0.7700810
[3,] 0.5930248 0.770081 1.0000000
$V
[,1] [,2] [,3] [,4]
[1,] 1.0000000 0.1671565 0.4472189 -0.4210630
[2,] 0.1671565 0.6778997 0.2886729 0.2235859
[3,] 0.4472189 0.2886729 0.8673512 0.3561256
[4,] -0.4210630 0.2235859 0.3561256 1.1370033
$var
[1] 2.559345
$iter
[1] 27
$tol
[1] 1.134173e-07
$logLik
[1] -1713.291 -1682.135 -1667.450 -1662.871 -1660.327 -1659.303 -1658.751
[8] -1658.501 -1658.369 -1658.307 -1658.275 -1658.259 -1658.251 -1658.247
[15] -1658.245 -1658.244 -1658.243 -1658.243 -1658.243 -1658.243 -1658.243
[22] -1658.243 -1658.243 -1658.243 -1658.243 -1658.243 -1658.243
$convergence
[1] TRUE
$call
MLmatrixnorm(data = A, row.variance = "AR(1)")There is a performance hit as fitting for these require calls to uniroot to find the zeros of the derivatives, but it is not so bad in the cases I’ve looked at.
library(microbenchmark)
res<-microbenchmark(
MLmatrixnorm(A),
MLmatrixnorm(A, row.variance="AR(1)"),
MLmatrixnorm(A, row.variance="CS")
)
plot(res, log="y", names = c("None", "AR(1)", "CS"),
col = c("darkred","royalblue","lightyellow"),
xlab="Variance Structure")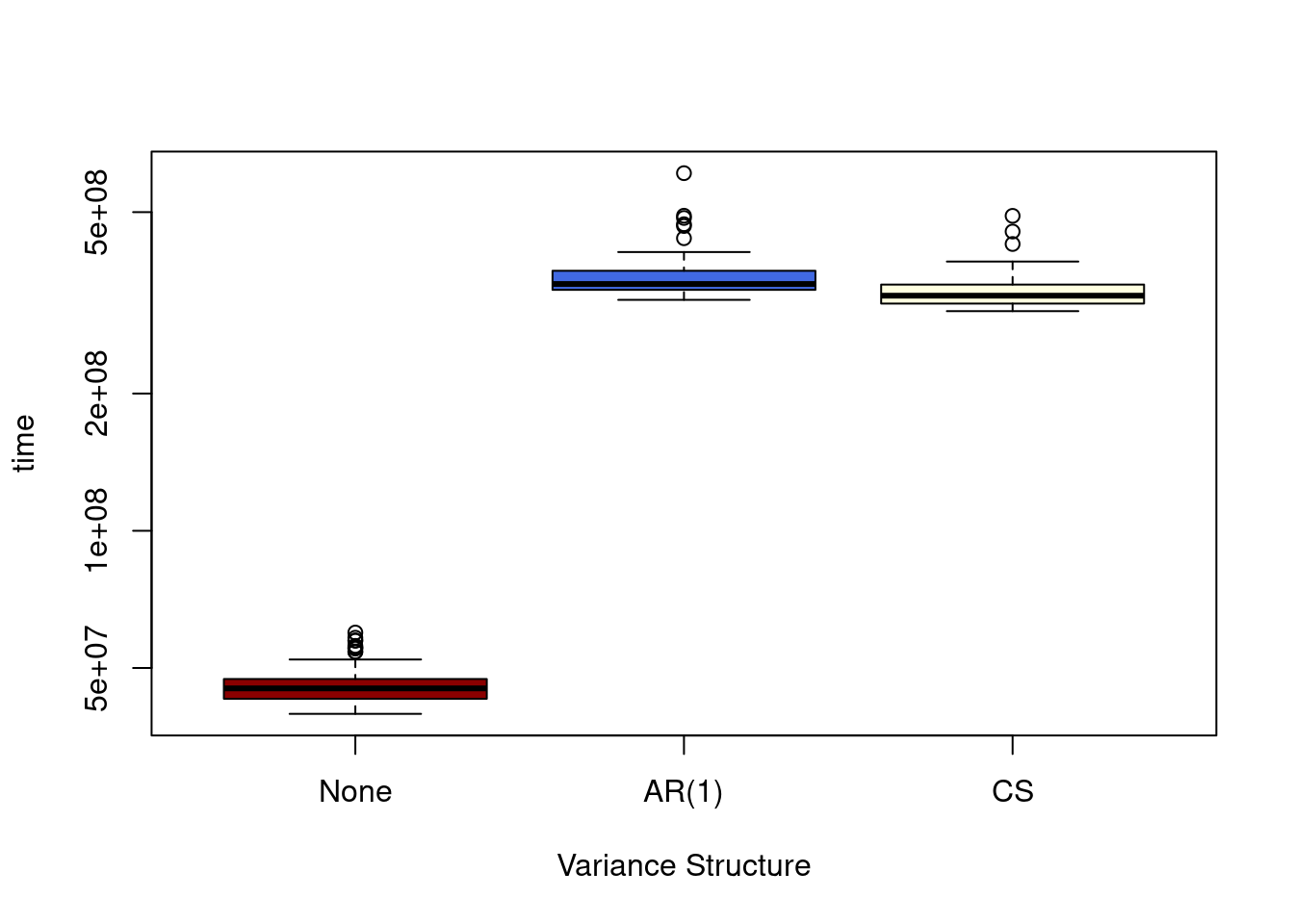
I will need to think hard about whether I want to add anything else first, as nobody wants to deal with massive updates to functionality in fast succession.
Here is a possible agenda:
- More distributions, such as skew \(t\)-distributions. I do not have much interest in matrix variate gamma distributions or beta distributions.
- Tools for working with matrix variate distributions, such as adaptations for LDA-type activities or clustering.
- Parameter estimation for distributions besides the normal distribution. \(t\)-distributions typically require use of EM or its extensions.
- The \(t\) distribution is parameterized differently between the matrix variate and multivariate cases - namely, a factor of \(\nu\). I changed it to be consistent with the multivariate case, but I probably should not have done so.